Modelo de datos: construcción de matriz de cardinalidades en R

Cuando se diseña una base de datos OLAP, hay que definir una tabla de hechos y unas tablas de dimensiones. En la definición de las tablas de dimensiones, es importante conocer las relaciones entre entidades para decidir el nivel de normalización de la información y evitar redundancia en el almacenamiento de datos.

HUGOMORE42

Para hacer esto es indispensable conocer la calidad entre entidades: si dos relaciones tienen una relación de 1:1, 1:m o n:m, y medir el grado de estar relación.

Usando R podemos visualizar de forma facil estas relaciones en una matriz de datos, que llamo matriz de cardinalidad. Esta matriz representa cuantos elementos de cada columna están contenidos en cada fila. O dicho de otra manera, cuandos valores distintos hay, en media en cada columna, para cada elemento de la fila.

Construiremos un ejemplo con la tabla de datos en csv que se puede descargar en la siguiente dirección https://github.com/chemadd/masterBD/raw/master/05.InteligenciaNegocio/IMF_M5_Mystery_Shopping.csv

Estos datos representan valoraciones de cuestionarios a oficinas de una empresa realizadas por un mistery shopper.

# librerias
library(tidyverse)
# library(kableExtra)

# carga de datos
dat <- read_csv2(url("https://github.com/chemadd/masterBD/raw/master/05.InteligenciaNegocio/IMF_M5_Mystery_Shopping.csv")) %>% 
  rename("FECHA_ENCUESTA" = `Fecha de ejecucion`) %>% 
  
  # nos quedamos solamente con una selección de variables para hacerlo más visualizable
  select(2:8)

head(dat)

## # A tibble: 6 x 7
##   NOMBRE_LOC          CP POBLACION    OFICINA PROVINCIA   COD_PROY ID_EVALUACION
##   <chr>            <dbl> <chr>        <chr>   <chr>       <chr>            <dbl>
## 1 MUCHAS BOIRO     15930 Boiro        910     "A CORU\xd~ 0267_001       1938117
## 2 "MUCHAS CARBALL~ 32500 "Carballi\x~ 910     ORENSE      0267_001       1938118
## 3 MUCHAS BUEU      36930 Bueu         910     PONTEVEDRA  0267_001       1938119
## 4 MUCHAS VIGO I    36202 Vigo         910     PONTEVEDRA  0267_001       1938120
## 5 MUCHAS REDONDELA 36800 Redondela    910     PONTEVEDRA  0267_001       1938121
## 6 MUCHAS VIGO II   36210 Vigo         910     PONTEVEDRA  0267_001       1938122

Se ha realizado una selección de las variables del data set original para que la representación sea más clara.

Pasamos a construir a partir de esta tabla, la matriz de cardinalidades. En primer lugar creamos una matriz de datos vacía con nombres de filas y columnas correspondientes a las variables del data.frame

cardinalidades <- matrix(nrow = ncol(dat), ncol = ncol(dat))
rownames(cardinalidades) <- names(dat)
colnames(cardinalidades) <- names(dat)
cardinalidades

##               NOMBRE_LOC CP POBLACION OFICINA PROVINCIA COD_PROY ID_EVALUACION
## NOMBRE_LOC            NA NA        NA      NA        NA       NA            NA
## CP                    NA NA        NA      NA        NA       NA            NA
## POBLACION             NA NA        NA      NA        NA       NA            NA
## OFICINA               NA NA        NA      NA        NA       NA            NA
## PROVINCIA             NA NA        NA      NA        NA       NA            NA
## COD_PROY              NA NA        NA      NA        NA       NA            NA
## ID_EVALUACION         NA NA        NA      NA        NA       NA            NA

Luego, para cada elemento calculamos la cardinalidad de la siguiente manera

De la tabla original se seleccionan solo las columnas correspondientes al elemento de la matriz que se está analizando. Una de las columnas de la tabla original corresponde a una fila de la matriz, y la otra de las columnas corresponde a una columna de la matriz.
Se eliminan valores duplicados de esta selección.
Se agrupan los valores correspondientes de la fila en la matriz de cardinalidades, y se realiza un conteo correspondiente al valor de la columna.

# creamos bucle que pase por fila y columna de la matriz
 for (fila in rownames(cardinalidades)) {
   for(columna in colnames(cardinalidades)) {

     # los valores de la diagonal (se compara la variable consigo mimsa)
     # tienen que ser 1
     if (fila == columna) {

       cardinalidades[fila, columna] <- 1
     }

     else {

       # asignacion de elemento de la matriz
     cardinalidades[fila, columna] <-

         # se selecciona del data.frame original, las columnas correpondientes
         # al elemento de la matriz que se está analizando
         dat %>%
         select_(fila, columna) %>%

         # se eliminan duplicados
         distinct() %>%

         # para la variable de la fila se cuentan los elementos que hay en cada columna
         group_by_(fila) %>%
         count() %>%

       # se calcula la media del contéo
       .$n %>%
         mean()

     }
   }
 }

cardinalidades <- round(cardinalidades, 1)
cardinalidades

##               NOMBRE_LOC    CP POBLACION OFICINA PROVINCIA COD_PROY
## NOMBRE_LOC           1.0   1.2       1.2     1.0       1.0      1.1
## CP                   4.4   1.0       2.0     1.1       1.0      3.7
## POBLACION            3.8   1.8       1.0     1.1       1.0      2.7
## OFICINA            523.2 152.8     167.1     1.0       8.3     57.8
## PROVINCIA          130.4  34.4      39.0     2.0       1.0     34.0
## COD_PROY            33.7  30.0      24.4     3.4       8.1      1.0
## ID_EVALUACION        1.0   1.0       1.0     1.0       1.0      1.0
##               ID_EVALUACION
## NOMBRE_LOC              4.9
## CP                     18.3
## POBLACION              16.0
## OFICINA              2522.8
## PROVINCIA             618.8
## COD_PROY              147.1
## ID_EVALUACION           1.0

Con esta matriz vemos por ejemplo que en media, cada PROVINCIA, contiene 34.4 codigos postales (CP) distinos.

Tenemos la matriz pero podemos darle un toque visual mas atractivo, que sirva a la vez para identificar los casos de cardinalidades más altas con un mapa de calor.

## preparacióon de los datos## 

 cardinalidades %>% 
  
            # transformacion en data.frame
            as.data.frame() %>% 
            
            # se elina la columna ID_EVALUACION: es la columna identificativa
            # de cada registro
            select(-ID_EVALUACION) %>% 
            
            # se introducen las filas de la matriz como una columna mas del data.frame, para poder emplearlas como variable en la visualización
            rownames_to_column("filas") %>% 
  
            # pivotacion de las tablas
            pivot_longer(names_to = "columnas", values_to = "cardinalidad", 2:ncol(.)) %>% 

  
  
## grafico ##
  
            ggplot(aes(x = filas, y = columnas)) + 
  
            # geom de mapa de calor. color en funcion de la cardinalidad
            geom_tile(aes(fill = -cardinalidad), colour = "white", 
                      size = 2) + 
            
            # se etiqueta cada celda con el nombre de la fila y la columna
            # de la matriz de cardinalidades
            geom_text(aes(label = columnas), color = "grey95", show.legend = F, alpha = 0.6, size = 3, nudge_y = -0.3) +
  
            # adicionalmente se etiqueta cada matriz con el valor de la cardinalidad
            geom_text(aes(label = round(cardinalidad, 1), color = cardinalidad),  fontface = "bold", show.legend = F) + 
  
            # eje de columnas arriba, a modo de encabezamiento
            scale_x_discrete(position = "top") +
  
            # tema del gráfico
            theme_minimal() +
            theme(axis.text.x = element_text(vjust = 0.5), 
                  axis.text.y = element_blank(), 
                  axis.title = element_blank()) + 
            labs(fill = "") + 
   guides(fill = FALSE)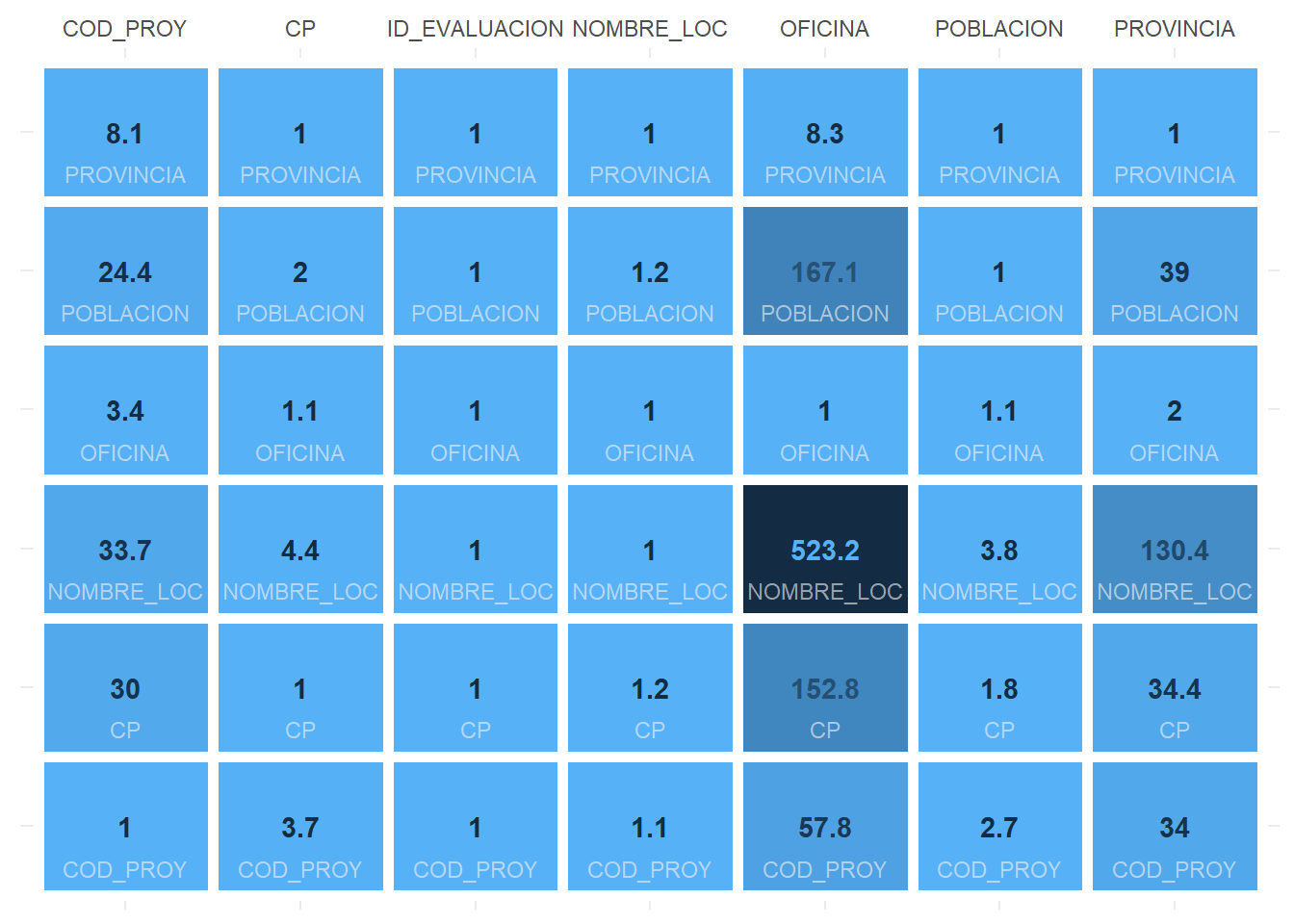

Tal como está visualizada la matriz ahora, cada elemento de la variable del encabezamiento contiene, el número de elementos de la variable etiquetada en la celda correspondiente.

Por ejemplo cada OFICINA tiene asignada en media 523.2 valores distinos para la variable NOMBRE_LOC

Modelo de datos: construcción de matriz de cardinalidades en R

Martín Pons